Python: Check if a Tree is Balanced (with explanation)

In this article, I want to talk about one of the most classic tree data structure questions.

It is also a very popular question during coding interviews.

Checking whether a binary tree is balanced or not.

I still remember very well that this was the first question I got asked during my first internship phone interview in my life.

Alright, before jumping right into the problem, I am going to assume you have some basic knowledge of data structures (specifically trees), analysis of algorithms, and recursion. If any of these topics are missing, I highly recommend filling in these gaps before proceeding.

First: The Definition of a Balanced Tree

The definition of a balanced tree is as follows:

A binary tree is balanced if for each node in the tree, the difference between the height of the right subtree and the left subtree is at most one.

Let’s look at some examples of balanced and unbalanced trees.

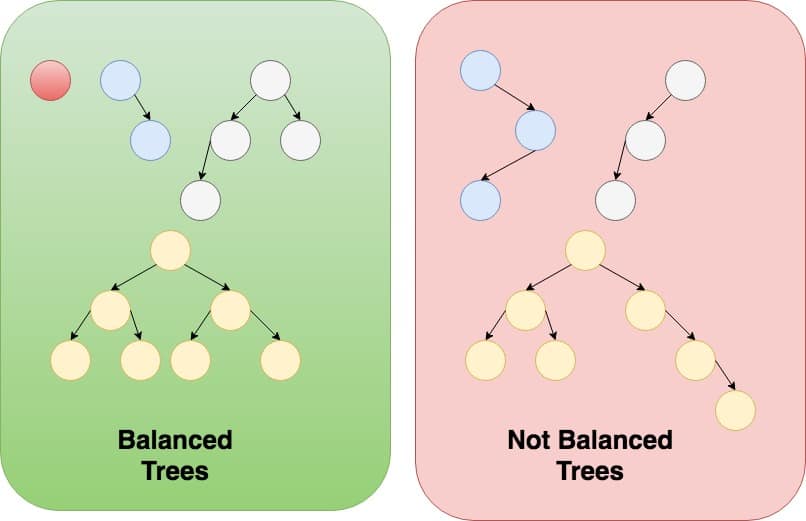
Second: Coming up with an Answer

Whenever I am faced with any tree data structure problem, the first thing I think about is to see if I can solve this problem recursively.

The reason is, tree data structures lend themselves very well to recursive solutions because, unlike python lists which have linear structures, trees have hierarchical structures.

It also turns out that if the problem actually has a recursive solution, this solution will be very simple and can possibly be just a few lines of code.

Always make sure you explore recursive solutions first before you jump into other alternatives when it comes to tree data structures.

So now the question is, “can we solve this question recursively?”

To answer this question, we need to find if we can solve our problem from the solutions of sub-problems.

In English, that would be: we are trying to find out if a binary tree is balanced, can we solve this problem from the solution(s) of the same problem but for smaller sub-trees?

Think about this, assume you know whether the right subtree and the left subtree are balanced, can you formulate a solution to the bigger original problem given the solutions of these two smaller subproblems?

The answer is definitely yes. Here is how.

From the definition of a balanced tree, we can conclude that a binary tree is balanced if:

1- the right subtree is balanced

2- the left subtree is balanced

3- the difference between the height of the left subtree and the right subtree is at most 1

With these steps in mind, you are ready to come up with your first solution to the problem.

Third: The Simple Solution

The simple solution to this problem is a direct implementation of the steps discussed previously.

Let’s define a recursive function is_balanced() that takes a root node as an argument and returns a boolean value that represents whether the tree is balanced or not.

Let’s also define a helper function get_height() that returns the height of a tree. Notice that get_height() is also implemented recursively

def get_height(root):
    if root is None: 
        return 0
    return 1 + max(get_height(root.left)\
    , get_height(root.right))

def is_balanced(root):
    # a None tree is balanced
    if root is None: 
        return True
    return is_balanced(root.right) and \
    is_balanced(root.left) and \
    abs(get_height(root.left) - get_height(root.right)) <= 1

The is_balanced() function returns true if the right subtree and the left subtree are balanced, and if the difference between their height does not exceed 1.

This solution will definitely do the job.

It is simple and easy to understand, but is it the most efficient?

Fourth: A Better Solution

There is nothing wrong with the simple solution.

But we are using two recursive functions: one that checks if a tree is balanced, and another one that returns the height of a tree.

Can we achieve the same goal by using only one recursive function?

Sometimes it might be useful to change the definition of the original recursive function, and come up with your own instead.

You see, most people, when faced with a recursive question, starts out by thinking about whether a solution of the original problem can be constructed from the solutions of subproblems.

In our example, the original problem was “write a function that takes in one argument, a tree root, and returns one boolean value”.

Sometimes it’s easier to modify the original problem a little to make it simpler or even more efficient, either by adding other arguments or returning other values.

Let’s redefine our recursive function is_balanced_helper to be a function that takes one argument, the tree root, and returns an integer such that:

1- if the tree is balanced, return the height of the tree

2- if the tree is not balanced, return -1

Notice that this new is_balanced_helper can be easily implemented recursively as well by following these rules:

1- apply is_balanced_helper on both the right and left subtrees

2- if either the right or left subtrees returns -1, then we should return -1 (because our tree is obviously not balanced if either subtrees is not balanced)

3- if both subtrees return an integer value (indicating the heights of the subtrees), then we check the difference between these heights. If the difference doesn’t exceed 1, then we return the height of this tree. Otherwise, we return -1

Awesome, let’s look at the code.

def is_balanced_helper(root):
    # a None tree is balanced
    if root is None:
        return 0
    left_height = is_balanced_helper(root.left)
    # if the left subtree is not balanced, then:
    # this tree is also not balanced
    if left_height == -1:
        return -1
    # if the right subtree is not balanced, then:
    # this tree is also not balanced
    right_height = is_balanced_helper(root.right)
    if right_height == -1:
        return -1
    # if the diffrence in heights is greater than 1, then:
    # this tree is not balanced
    if abs(left_height - right_height) > 1:
        return -1
    # this tree is balanced, return its height
    return max(left_height, right_height) + 1

With the help of the above function, finding a solution to the original problem is a piece of cake.

if is_balanced_helper returns a number that is greater than -1, the tree is balanced.

Otherwise, it is not.

def is_balanced(root):
    return is_balanced_helper(root) > -1

Fifth: Time Complexity

It is easy to come up with the time complexity of iterative solutions.

Most of the time, if you only have one loop, the complexity is O(n)

Two nested loops? no problem. O(n^2)

Three nested loops? Piece of cake. O(n^3)

It becomes a little tricky though when you want to analyze recursive algorithms.

There are essentially two ways to analyze the complexity of recursive algorithms.

First: You can draw a recursion tree and follow the recursion tree one level at a time until you find out the complexity.

Second: You can use the Master theorem to quickly find out the complexity.

I highly recommend you study the recursion tree method and the Master theorem before you move on.

If you get asked about the time complexity of this problem in an interview, and you haven’t memorized the Master theorem by heart (which is totally normal by the way), let your interviewer know that you are familiar with the Master theorem or even better try to draw the recursion tree and deduce the complexity on the spot.

Alright, without further ado, let’s try to analyze the complexity of our solutions.

Analyzing the simple algorithm

I am going to use the Master theorem to analyze both algorithms.

Let’s revise the steps of the simple solution.

To find if a tree of size n nodes is balanced:

1- Solve the same problem for the right subtree

2- Solve the same problem for the left subtree

3- Get the heights of the left and right subtrees

The worst case scenario in terms of time complexity will happen when the tree is actually balanced because this will result in the maximum number of operations.

If the tree is balanced, then you can safely assume that the right subtree is approximately half the size of the whole tree, and the left subtree is the other half.

Another thing, notice that getting the height of a tree has an O(n) complexity. get_height() is also a recursive function and you can use the Master theorem to get its complexity as well. I will leave this for you as an exercise.

Now, we can put our algorithm in a form that will allow us to use the Master theorem.

T(n) = 2 * T(n / 2) + o(n)

In English, you can read the above as “in order to solve the original problem of size n (the original tree), we had to solve two subproblems of size n/2 (the right and left subtrees), and then we had to get the heights (which has O(n) complexity)

If you’re familiar with the merge sort algorithm, the above formula is exactly the same as that of merge sort. The Master theorem states that the complexity of algorithms that can be expressed in the above formula is O(n log n).

Analyzing the efficient algorithm

Analyzing the complexity of the efficient solution is much easier.

After calling our recursive functions on the right and left subtrees, no extra processing is really required (except for some comparisons which are O(1)).

This means that you just visit each node of the tree once and that’s it, resulting in an O(n) complexity.

You can also use the Master theorem to arrive to the same result.

This time our formula is:

T(n) = 2 * T(n / 2) + o(1)

Applying Master theorem on the above formula results in an O(n) complexity.